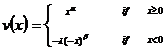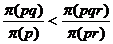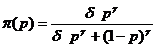Tversky, A. & Kahneman, D.（1985）The Framing of Decisions and the Psychology of Choice. In George Wright（ed.）Behavioral Decision Making. Plenum Press, New York, 25-41.
1.緣起
長久以來，經濟學處理風險及不確定問題時，均會使用期望效用理論。就一規範性理論的範疇而言，這個理論是非常令人驚異的，因為它告知我們人如何在風險之下做決策，但就實証性理論的範疇而言，則不那麼令人激賞了，因為人們似乎沒那麼理性，也不會使用那麼多的數學工具，並且有許多做決策時產生的現象仍無法解釋。
在經過多年的找尋後，兩位學者Daniel Kahneman及Amos Tversky發展出展望理論（Prospect Theory）。這個理論與期望效用理論不同的是，決策者是在各項被包裝過的展望（Framed Prospects）中選擇一個。由於這個理論的出現及使用，說明了原本期望效用理論無法解釋的現象，並且為經濟學開拓了行為經濟學的視野及為心理學者開展了生理心理學的領域，可以說是貢獻非常大，現在我們來看看這個理論是如何運做的。
2.內容大要
2.1人們行為的不一致性
所謂的決策可以說就是選擇，也就是說在事件的出象及出象的機率都知道時，由可行的方案中選擇一個。在展望理論中，對於人們行為的處理方式則有所不同，作者首先定義了決策框架（Decision Frame），說明決策者對某一個特定選擇的行動方案、報酬及情境的認知，決策者所選擇的框架一部份是由問題的形成所控制，一部份是由規範、習慣及決策者的個人特徵所決定的。
通常在經濟學的理性決策假設下，偏好是不會隨著問題包裝（frame）方式的不同而改變的，但事實上，人的偏好會隨著方案、情境及出象的包裝不同而改變的，試看下面二例：
問題一：（訪問152人）假想亞洲爆發罕見疾病，預見會有600人死亡，有方案a及方案b可供選擇以對抗疾病，估計如下：
方案a：200人可以獲救 【72%】
方案b：1/3機率600人可獲救，2/3的機率無人可獲救 【28%】
請問方案a與方案b您喜歡那一個？
結果一如括號所示，方案a獲得了大多數人的支持，這就是風險趨避（risk averse），確定200人可獲救的方案比較吸引人。
問題二：（訪問155人）同於問題一，但是陳述的方式不同：
方案c：有400人會死亡 【22%】
方案d：有1/3的機率無人死亡，2/3的機率600人均死亡 【78%】
請問方案c與方案d您喜歡那一個？
結果方案d獲得高度支持，這是風險喜好（risk taking）的情形。
我們顯然可以看出，問題一與問題二只是描述的方法不同，但事實上是相同的。問題一以正面敘述法，以獲救人數詢問，而問題二用反面敘述法，用死亡人數詢問，結果竟然是如此的不同。這就說明了在有利得時，人們常是風險趨避的，而在有損失時，人們常是風險喜好的，傳統的期望效用理論的應用顯然是出了問題，於是有必要建立一個新的理論說明這個現象。
2.2展望理論的內涵
展望理論的內涵區分為下面二部份：
價值函數（The value function）：
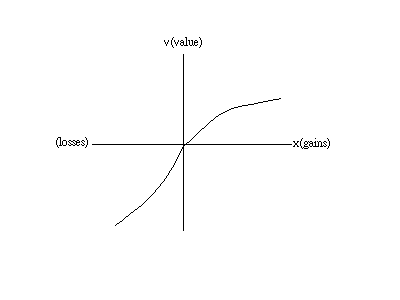
人們在有利得（gains）時，會隨著利得的增加，而價值是遞減的，表現出風險趨避的特性；若有損失（losses）時，則隨著損失的增加，所造成的價值減少是遞減的，這表現出風險偏好的特性，這通稱為敏感性下降法則（The Principle of Diminishing Sensitivity），或韋伯－佛契納法則（Weber-Fechner Law）。另一方面，人們會對失去錢的反應會較有利得時為激烈，價值函數及圖形如下所示：
（1）
其中，α及β介於（0，1）之間的數，λ>1，當x>0時表示為利得，x<0時表示為損失。依實証研究的結果，α＝β≈0.758，而λ≈3.11。
圖一：價值函數圖形
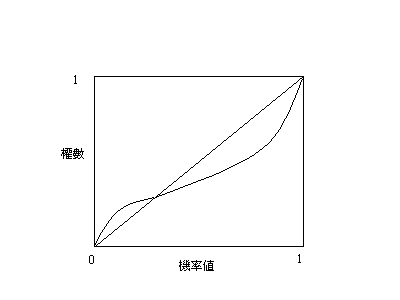
權數函數（weighting function）：
π（p）是決策權數，為機率值p的單調遞增函數，這個函數有下列特點：
（1）不可能的事件拾棄，即π（0）＝ 0，由於函數經過標準化（normalized）處理，使π（1）＝ 1。
（2）機率低時給予較重的權數，機率較高時給予較低的權數。
（3）
，其中0＜p及q，r≦1。
權數函數及圖形如下：
（2）
其中，依實証研究指出δ≈0.77，γ≈0.69。
圖二：權數函數圖形
依上面所述，我們可舉一例子說明，例如
的成立便符合前述權數函數的特性。
我們可以得出展望價值為：
V＝π（p）V（x）＋π（1－p）V（x）
我們現看看這個新分析工具如何使用。
2.3決策分析
2.3.1方案的包裝
現在我們看看下面兩個例子：
問題三：（訪問150人）想像下列成對方案同時發生，您選擇那一項？
第一對：方案a：確定獲得$240 【84%】
方案b：25%機率可獲得$1000，75%機率可獲得0 【16%】
第二對：方案c：確定損失$750 【13%】
方案d：75%機率會損失$1000，25%機率會損失0 【87%】
多數回應者在第一對中選擇了方案a，表現出風險趨避的特性，而在第二對中，多數回應者選擇了方案b，表現出風險偏好的特性。此時便可以使用展望理論中價值函數是S型來解釋，因為價值函數假設了有利得時是風險趨避，而有損失時則是風險偏好，現在我們試看問題四：
問題四：（訪問86人）
方案a及b：25%的機率可獲得$240，75%的機率會損失$760 【 0%】
方案b及d：25%的機率可獲得$250，75%的機率會損失$750 【100%】
在問題四中，明眼人一看就可知方案b及d的組合較好，但為何在問題三中，反而看不出來呢？這就方案包裝後所產生的效果。其實，此題共可有四種組合，分別為（ac）、（bc）、（ad）、（bd），而回應者撰擇（ad）的組合較多，但事實上則是（bc）的組合較佳。
2.3.2情境的包裝
現在我們試看問題五、六及七：
問題五：（訪問77人）請問方案a及方案b您喜歡那一個？
方案a：確定獲得$30 【78%】
方案b：80%機會獲得$45 【22%】
問題六：（訪問85人）下列需經過兩個階段
第一階段：75%的機率無任何結果，25%的機率會進行到第二階段
第二階段：方案c：確定可獲得$30 【74%】
方案d：80%機率可獲得$45 【26%】
問題七：（訪問81人）請問方案e與方案f您喜歡那一個？
方案e：25%的機率可獲得$30 【42%】
方案f：20%的機率可獲得$45 【58%】
在問題五、六及七中，事實上，問題六與七是相同的，若是問題六到了第二階段，則等於是回到了問題五，是以我們可以說問題五、問題六在邏輯上是相同的，而問題六與問題七在邏輯上是相同的，然而回應者對問題五及問題六的反應是相似的，而對問題六及問題七的反應則是不同的，這便引出了所謂確定效果（certainty effect）及假確定效果（pseudo certainty effect）的問題。
確定效果就是艾萊士的矛盾（Allais’s Paradox），這位於一九八八獲得諾貝爾經濟學獎的法國經濟學家於一九五三年首度提出這個現象，他發現當事件出象的機率值突然由高機率值陡降至低機率值時，雖然出象的貨幣期望值相同，但人們的決策反而出現了不一致的情形，一如問題五及問題七所顯示的，人們會偏好於事件出象的機率愈確定的情形，這在經濟學中傳統的期望效用理論完全是無法解釋的，但我們卻可以使用展望理論加以解釋。
在展望理論中，權數函數表現了人們的行為會有這樣的特性，即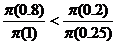
，故利用這個特性便可以解釋了艾萊士的矛盾。因為在問題五中，多數的人偏好確定能得到$30而不喜歡有0.8的機率可得到$45，也就是這個w（0.8）v（45）<
w（1）v（30）式成立；而在問題七之中，多數的人偏好0.2的機率得到$45，而不喜歡有0.25的機率得到$30，也就是說，下列等式成立，即w（0.25）v（30）<
w（0.2）v（45），我們將這兩個不等式放到一起，整理便可得到式成立，如此便可以解釋艾萊士的矛盾。
而在問題六及問題七之中，則是反映了假確定效果，因為看起來，問題六的$30比問題七的$30更為確定，事實上是假象，因為問題六及問題七在邏輯上是相同的，但是回應者卻被蒙蔽了。這可以引申一個有趣的現象，即當機率值由0.01降到0時，相對於機率值由0.02降到0.01時，人們會給予較高的評價，我們可以將此應用到保險，試看下例。
在日常生活中，人們的行為類似機率保險（probabilistic insurance），其意為獲保險理賠是具某些機率的。如被保險人只需付一半的保險費，若在單數日被保險人出事，則被保險人需付清另一半的保險費，而保險公司負責賠償所有損失，但若在雙數日被保險人出事，則保險公司退回已付的保險費，由被保險人自行負擔所有的損失。而根據受訪結果，95名參與者只有20%接受，而80%拒絕，這意味著同樣是降低機率，由50%降至0%的價值會大於100%降至50%。
2.3.3出象的包裝
試看下面問題八及問題九。
問題八：（訪問183人）若已決定要花$10元買門票看電影但尚未買票，進入戲院後卻發現丟了$10
方案a：願意再花$10買門票者 【88%】
方案b：不願意再花$10買門票者 【12%】
問題九：（訪問200人）若已花$10買門票進入戲院後發現丟了門票
方案a：願意再花$10買門票者 【46%】
方案b：不顠意再花$10買門票者 【54%】
其實問題八及問題九皆花費了$20，但是在問題九之受訪者卻覺得要花$20買一張門票（因已買票卻遺失票），但在問題八之受訪者卻覺得只要花$10買門票（因尚未買票而遺失錢），所以人們會偏好於問題八，這就是出象包裝的效果，也反應了人們心理記帳（psychological account）方式的不同。
問題十：買物品問題。
方案a：假想您要買一件夾克要$125、計算機要$15、若在20分鐘車程遠的地方計算機只要$10，則則願意到20分鐘車程遠的地方買計算機的機率為68%。
方案b：假設買一件夾克要$125、計算機要$15、若在20分鐘車程遠的地方夾克只要$120，則願意到20分鐘車程遠的地方買夾克機率為29%。
雖然方案a及方案b皆省了$5，但是受訪者認為節省在計算機效用較節省在夾克的效用大，此亦為心理記帳的差異，感覺便宜折數不同，此現象與消費者理性假設是矛盾的。
3.管理意涵
作者提出了有別於傳統期望效用理論的展望理論。在此十個問題之中，我們可以發現人們在風險及不確定下做決策時，其實不像期望效用理論所提及的是完全理性，反而會受到問題的描述方法差異而產生前後不一致的情形，這也是作者所說的問題包裝方式不同所造成的結果，而此展望理論在解釋人們行為方面有很大的效果。
此研究可以供決策者參考，當面對複雜的問題時，是否僅只憑感覺下決定，而沒有詳審各可行方案、出現的機率及報償。此外，輸贏結果表達的方式也會引起心理面不同的反應，相信大家都瞭解「屢敗屢戰」及「屢戰屢敗」給人感覺的差異。
對事件結果的決策構思過程也可以反映一個人對結果的接受程度，進而可以用來做為自我控制的工具，而決策者可以知道在決策的過程之中會受到多方面的影響，而無法完全理性，是以必需要審慎處理決策過程之中的諸多矛盾現象。
而決策者在面對各式各樣的競爭對手，必也知曉對手也會受到決策過程之中各種包裝不同而產生不同的結果，是以決策者操弄包裝方式也可以應用為策略的工具，此即孫子所言「兵者詭道也」，管理者可以廣泛在決策時應用這個理論。
Topic6 –2: The Framing of Decisions and the Psychology of Choice.
第二週讀書心得報告：企博一 9041811 鄭國枝
一、簡介
本文上週已做過一次心得報告，對展望理論之大意及日後博士學位論文之應用想法初步之想法。本週心得報告進一步對展望理論中與該觀念息息相關之概念簡單介紹。除此之外，因本文為行為財務及會計學之濫觴，故本週再精讀本文後除大膽批評本文外，其他亦引發諸多論文上心得想法，諸如應用在我國財會計主管會計政策之決策理性及投資者在股市多頭空頭投資行為之探討等。
二、與本文相關之重要概念
K&T 將這些違反傳統理論的部份歸納出下列三個效果來說明：
（一 ）確定效果(certainty effect)
此效果是指相對於不確定的出象(outcome)來說，個人對於結果確定的出象會過度重視。KT 設計了兩個問題來說明確定效果。第一個問題是，假設有兩個賭局如下：
實驗設計：K&T訪問77人，方案a及方案b之不同決策選擇比例？
方案a：確定獲得$30 （期望值為$30）； 【78%選擇該方案】
方案b：80%機會獲得$45 （期望值為80%×$45＝$32）【22%選擇該方案】
確定效果就是艾萊士的矛盾（Allais’s
Paradox），這位於一九八八獲得諾貝爾經濟學獎的法國經濟學家於一九五三年首度提出這個現象，他發現當事件出象的機率值突然由高機率值陡降至低機率值時，雖然出象的貨幣期望值相同，但人們的決策反而出現了不一致的情形，一如上述實驗設計顯示的，人們會偏好於事件出象的機率愈確定的情形，這在經濟學中傳統的期望效用理論完全是無法解釋的，但我們卻可以使用展望理論加以解釋。
（三 ）分離效果(isolation effect)
若一組prospects 可以用不只一種方法被分解成共同和不同的因子，則不同的分解方式可能會造成不同的偏好，這就是分離效果。KT
設計了一個兩階段的賭局來說明分離效果。
實驗設計二：（訪問85人）下列需經過兩個階段
第一階段：75%的機率無任何結果，25%的機率會進行到第二階段
第二階段：
方案c：確定可獲得$30。（期望值為25%×$30＝$7.5）【74%選擇該方案】
方案d：80%機率可獲得$45。（期望值為25%×80%×$45＝$9）
【26%選擇該方案】
實驗設計三：（訪問81人）請問方案e與方案f您喜歡那一個？
方案e：25%的機率可獲得$30 。（期望值為25%×$30＝$7.5）
【42%選擇該方案】
方案f：20%的機率可獲得$45 。（期望值為25%×80%×$45＝$9）
【58%選擇該方案】
實驗設計二與實驗設計三事實上是相同的，由前述結果，大部份的人會選擇前者。由此可知，在兩階段的賭局當中，個人會忽略第一個階段只考慮到第二個階段的選擇，即是有短視(myopia)的現象。在這種情況，個人面臨的是一個不確定的prospect
和一個確定的prospect若只考慮最後的結果和機率，個人面臨的是兩個不確定的prospects雖然這兩種情況的預期值相同，但是由於個人不同的分解方式，會得到不同的偏好。由此可知，若以預期效用理論的觀點來看，這兩個賭局是相同的，個人的選擇應該相同。但是實際上卻不是如此，個人會因為問題描述方式的不同而有不同的選擇，這就是所謂框架相依的現象
。
（三）心理帳戶（psychological account）
K&T 所討論的主要是單一賭局的選擇，但是個人實際上常常是同時面對多個賭局。例如，投資者在買賣股票時，可能會同時買進或賣出多種不同的股票。據此，Kahneman
and Tverskey (1981)認為個人對於多個不同賭局的反應，必須視為一種心理帳戶(mental
account)之表達。所謂心理帳戶，即是指每個人皆根據其自身的參考點，訂出一個決策的方案。例如：不同的股票，在買進時便有不同的參考點，而投資人面對此一現象，便會根據其自身之心理帳戶作出最適的決策。
實驗設計四：（問卷人數183人）若已決定要花$10元買門票看電影但尚未買票，進入戲院後卻發現丟了$10。
方案g：願意再花$10買門票者【88%選擇該方案】
方案h：不願意再花$10買門票者【12%選擇該方案】
實驗設計五：（訪問200人）若已花$10買門票進入戲院後發現丟了門票
方案i：願意再花$10買門票者。【46%選擇該方案】
方案j：不顠意再花$10買門票者。【54%選擇該方案】
其實實驗設計四及五皆花費了$20，但是實驗設計五之受訪者卻覺得要花$20買一張門票（注意：因已買票卻遺失票），但在實驗設計四之受訪者卻覺得只要花$10買門票（注意：因尚未買票而遺失錢），所以人們會偏好於實驗設計四，這就是出象包裝的效果，也反應了人們心理帳戶（psychological
account）方式的不同。
實驗設計六：買物品問題：假設買一件夾克要$125、計算機要$15。
方案k：若在20分鐘車程遠的地方計算機只要$10（節省五元），則願意到20分鐘車程遠的地方買計算機的機率為68%。
方案l：假設買一件夾克要$125、計算機要$15、若在20分鐘車程遠的地方夾克只要$120（亦節省五元），則願意到20分鐘車程遠的地方買夾克機率為29%。
雖然方案a及方案b皆省了$5，但是受訪者認為節省在計算機效用較節省在夾克的效用大，此亦為心理記帳的差異（雖然皆便宜五元，但心理記帳夾克便宜1/5，計算機便宜1/25），感覺便宜折數及程度不同，此現象與消費者理性假設是矛盾的。
三、對本文評論與應用
（一） 對本文之評論
1.忽略人們行為雖不完全理性但可透過討論量化得出較理性之結果
K&T提出了有別於傳統期望效用理論的展望理論，指出人們在風險及不確定下做決策時，不像期望效用理論所提及的是完全理性，因而會受到問題的描述方法差異而產生前後不一致的情形。但事實上重大決策之制訂是可透過龐大幕僚群群策群力或利用資訊科技精密之量化得出正確決策。
2.利用展望理論之激勵策略
事實上可利用問題包裝或如展望理論之分離效果訂出激勵策略，如分離效果之實例：日本松下公司在石油危機不景氣年代，公司當局放出原本年終獎金從近十個月可能無法發出任何獎金，甚至裁員訊息，但結果公司不但未裁員且發出正常年終獎金，員工末不感激，於是公司上下一心將公司存貨全部推銷完畢，並反常在不景氣中業績一枝獨秀。
（二） 對本文應用研究之新想法
1. 設計會計政策或盈餘操縱實驗設計，調查台灣實務界財會主管是否做出理性決策：
在民國87年以來，上市公司因管理當局會計舞弊致使公司財務陷於危機層出不窮，造成股市動盪，國家經濟受到極大衝擊，其茅頭直指管理當局。由於管理當局之政策失當，會計政策之制訂可能具有非理性之現象。故本文激發論文想法，可對實務界會計主管可進行展望理論實驗設計進行問卷，以探討我國財會管理者之會計決策是否符合理性行為。
2. 以我國上市公司資料實證證實投資行為之非理性行為
吾人可從股市極熱（多頭市場）股市交易量極大，及股市低靡（空頭市場）股市交易量極小。但就投資觀點歷史證明股市低點方有獲利機會，股市位於高點易使投資者損失慘重，探討該非理性行為實為研究方向之一。而如股市時值多頭期間，投資者買賣交易頻繁，但空頭期間投資者雖已血本無歸，但仍執意握有股票，不認賠殺出；此外專家常常建議投資者建立停損停益點點，但實務上確是停益容易停損難，這些問題投資者種種不理性投資行為，目前我正思考如何用展望理論加以解釋。
