当学者们描述或解释某种现象时,他们对以下三种类型的认知结构的依赖各不相同:数学概念和方程式,语义网络和基于感性的图式表征(schematic representations) 。在古代希腊,√2原来的意义包含一种可感知的特征,因为它指的是具有一定单位长度的三条边构成的直角三角形斜边的长。大部分当代数学系的学生都以为√2代表一个没有图式成分的无理数的抽象概念。罗莎琳德·富兰克林(Rosalind Franklin) 对力学模型结构(construction of mechanícal models)的反感可能曾是克里克(Crick)和沃森(Watson) 发现脱氧核糖核酸结构的一个原因。当这两个人得以在四种碱基(bases)中看到可能存在的空间关系并以示意图的方式来思索它们的存在状况时,他们的想象力提高了。
“具体”和“抽象”这两个词,其描述的是两种语义概念的类型,可以用对一个现象进行某种语义的和图式表征的微分比例(differential proportion)的描述来取代。这就是说,称之为“具体”的语义网络总是包含着各种图式(即一个苹果的可感知的表达通常是水果的语义网络的组成部分)。像“形而上学”之类的抽象概念的网络,即使有什么可感知的图式(schemata),也是很少的。当克里克和沃森在他们1953 年的著名论文中画出基因的结构时,“基因”这个概念就得到了一个图式的特征。图式节点(schematic node)的添加并未使基因这个概念变得更具体,较不抽象,更确切地说,它给一个曾经是抽象的语义网络添加了一个图式或图解(schema) 。
语义的表达和图式的表达有不同的结构( organizations) 。它们中一个显著的差别,至少对说英语的人来说,是你在遇到一个物体时,其通常的背景表达(representations)总是与该事件的图式相联系。比如,一只鸟的图式很可能与树木、草地和天空的图式联系起来。相比较而言,语义网的结构着重于概念层次(hierarchies)、反义词和各个概念的特征。所以与“鸟”这个词结合得更密切的是知更鸟、动物、翅膀这些词的语义节点(semantic nodes) ,而不是树木、草地和天空这些词的语义节点。图式这个词没有对立物——甜味的图式与酸味的图式没有联系——它们并不相互套入(nest)构成不同的层次。此外,某种图式原型(schematicprototype) ,比如一个朋友的脸的图式原型,使辨别朋友脸上各种表情之间的微妙变化变得很困难,因为引起变化的力量保用于整个脸而不是各个单独的部位。相较而言,一个女人关于一个朋友的语义网,包括名字和许多特征在内,并不意味着她不能区分这位朋友的各种心情。
在童年早期,可感知的经验的图式的建立,常常早于语义的表现形式(semanticfonns)。1岁的儿童在学会基数的语义表现形式前就己感知脸上的一双眼睛和一个鼻子的图式。此外,图式常常影响各个相关的语义网,但相反的情况较不普遍。这就是说,某一类经验的图式受语义表现形式影响的可能性较小。这种不对称,在成年人估计在显示器的屏幕上长短不等的线条所停留的时间时,得到了证实(持续时间按照从1 秒到5 秒钟排列起来)。语义对屏幕上线条停留时间的估计受到线条长度的影响——较长的线条被估计的时间也较多。但对各种线条长度的估计不受该线条在屏幕上停留时间的影响。该观察结果意味着“时间”的语义概念与一根线条的长度或两个地点之间的距离的图式相联系,但长度或距离的图式受时间的语义概念影响的情况较少发生。虽然爱因斯坦广义相对论的方程式在一个“空间—时间扭曲” (space-time warp)的理论上把空间和时间结合起来,但大部分学者仍继续把时空观念分开来理解。
许多能够从1 背到10 的三岁的孩子还不理解10 这个词所指的数量比5 大,当他们瞪着一个盘子里放着的甜饼干并听到某个人说10 或5 这两个词时,他们对盘子里的10 片和5 片饼干的图式不会受到影响。所以,年幼的孩子对盘子里5 片饼干的图式,不意味着他拥有某种关于数量的概念。从1 背涌到10 类似于孩子吟诵音阶的音符名称的能力。两种情况都是死记硬背地学习某个序列(sequence)的结果,但他们不理解语义的意义。然而,不同的量的图式确实有助于学龄前儿童学习基数的意义。
人类学会把一株树的树冠的图式与关于未来和上帝(the Divine)的语义网联系起来,把树的根部的图式与关于过去和魔鬼的语义网联系起来。与一种甜食或温暖的火光一起产生的各种感觉状态(sensory states)的图式是善(g∞d)的语义网的组成成分;而苦昧和痛苦是恶(bad)的语义网的组成成分。一个向自我或向另一个人挑衅而产生的忧虑,很可能与关于公平和正义的语义网有关。简单地说,首先发展起来的各种可感知的经验的表达,常常被用作脚手架,以扩大抽象的语义术语(semantic terms)的意义。如果一份技术报告包含着一幅大脑的图片,而另一份报告只展现数据,并非专业神经科学家的大学生可能会更相信前者的结论。在判断一个因一桩严重的罪行而受到审判的人是否为精神病患者时,如果辩护律师出示被告大脑的图片,并指出其大脑与大部分人的大脑不一样,所以不能完全为他的行为负责,这时陪审员也很容易接受律师的意见。或许这就是为什么为普通读者写作的弦理论家(string theorists) 要加上一幅图,表示一根弦看起来可能像什么东西,即使作者们都知道用图来解释那些关于弦的数学方程式是不可能的。作为一个成年人,我相信用言辞和用数学公式证明地圆说的论点,但我猜想,如果新的证据使科学家们改变他们的见解,我可能被他们说服而改变我的想法。但当我看见太空船拍摄的我们星球的图片,我对于地球是圆形的这一信念就变得不可动摇了。一图确实胜千言。
数学概念
在笛卡儿和牛顿极其成功地证明各种数学命题后,微分对三种类型的心智工具的解释能力,在17世纪的欧洲变得清晰。自然哲学家开始声称,各种方程式将会取代各种图解和语义的描述,这在任何时候都是可能的。数学形式(Mathematical forms)已经被证明在物理学和化学中极其有效。维尔纳·海森堡(Werner Heisenberg)创造性地使用代数矩阵(algebraic matrices)发现了著名的测不准原理(uncertainty principle ,或译“不确定性原理”)。许多物理学家,包括爱因斯坦,开始时都抵制海森堡的论点,因为该论点否定了严格的决定论。难以想象,没有什么词语能够准确地描述各种矩阵所展现的物理现象。梅森堡的导师尼尔斯·玻尔(Niels Bohr)更喜欢把语义概念与电子绕着质子和中子的原子核旋转的图式结合起来思考。令人惊讶的是,玻尔的研究笔记上只有图片和词语,但没有数学计算。当玻尔在1939年第一次听说铀原子裂变的消息时,他试图通过想象一滴往下落的球形的水滴(代表原子核)因受到中子的轰击而变形为一颗花生的形状来理解这种惊人的现象。玻尔关于一颗被加热的原子散发出来的的光谱线和绕着它转的电子能量之间的关系的洞见,是某种直觉而不是用方程式进行运算的结果。
保罗·迪拉克(Paul Dirac)也是通过数学术语来思考的一个英国的物理学家,他的一篇评论通过比较海森堡所偏爱的工具和玻尔所偏爱的工具,揭示了两者的差异。1826年,迪拉克曾在哥本哈根拜访过玻尔,玻尔坚持使用那些基于定性的语义概念的论点,而不是较不含糊的各种数学方程式,这使迪拉克产生了挫折感,因为后者是英国科学家认为在心理上比较容易操作而且让人感到满意得多的方法。当与被尔一起参观一场艺术展览时,迪拉克注意到莫奈的一幅画中一条小船旁边有一点暗灰色的、模糊的颜料,于是说道:“这点是不合理的。”乔治·盖莫(George Gamow) 是一个物理学家,在克里克和沃森描述脱氧核糖核酸的结构前就设想脱氧核糖核酸是一套编码,他提供了一个有说服力的例子,说明一个科学家所偏爱的思维工具如何得以干扰一次发现。因为对称(意思是没有改变物体形状的一次数学运算)在物理学中是一种基本概念,盖莫假定信使核糖核酸(messenger RNA)辨认脱氧核糖核酸分子,不管是从左到右还是从右到左都不会有什么区别。然而,核糖核酸具有某种极性(polarity) ,而信使核糖核酸只从一个方向来辨认脱氧核糖核酸的编码。所以,盖莫未能推断出该分子的正确分子结构。尤金·威格纳(Eugene wigner)是另一个通过数学结构思考问题的物理学家,他指出他的分析意味着生命形式绝对不可能从化学元素中产生。凯尔文勋爵(Lord Kelvin)是不是19世纪最受尊敬的自然科学家暂不作论,但他恐吓达尔文,说他的数学分析证明地球不可能那么古老,所以不可能支撑达尔文的理论主张。
有些儿童很难把数学表达(representations)与较熟悉的词语的表达区分开来。卡尔·荣格(Carl Jung)曾提供了一个心理障碍(psychological block) 的例子。他回忆起自己小时候完全没有能力接受这样一个论点:如果a=b并且b=c,那么a=c ,因为他总是用各种语义的概念来取代各个字母的符号,并厌恶以下这种可能性:如果猫=宠物并且宠物=狗,那么猫=狗。“我的智力道德反抗这些古怪的矛盾事物,这永远阻止了我理解数学。”荣格遇到的困难是可以理解的。在一个方程式中的一个字母可以代表任何种类(class)的一系列现象的数值,这个观念的出现还只有12个世纪。此外,某些语言用不同的名称来称呼等量的不同性质的物体。比如,斐济(Fiji)东部岛屿的居民称100 条独木舟为博拉(bola) ,称100颗椰子为科拉他(kora)。我认为人类历史上后来出现的代数学意味着,与语义表达或图式表达的操作不一样,用各种抽象的数学概念来推论的能力,不是一种生物学上已经准备好的、轻易地来自人类直觉的能力。记住,几何学的出现早于代数学许多世纪。伯特兰·罗素在11岁第一次读过欧几里得(Euclid) 的书后就爱上数学的这种情况是罕见的。
不是所有的现象或所观察事物之间的关系都适合于用数学来描述(mathematicaIdescription) 。盛有陈酿的水桶以及酒香、酒味之间的关系就是一例:而且,两个或多个概念之间的某种数学关系不能解释上述关系。考虑一下一个苹果从离地6英尺高的树枝落到地面上的情形。你可以把这事拍成电影,用词语来描绘,或写出数学公式s= 1/2gt2来显示苹果所穿过空间的距离等于地心引力与下落时间的平方的乘积的1/2 。这三种描述方法都不能解释为什么苹果会以这种方式落到地面上,物理学家还不知道地心引力的本质。然而,数学模型具有优势,它表示得更清晰,有希望应用于某个物体落到地面上的所有场合。所以,大部分科学家同意,与另两种形式相比,数学陈述(mathematical statements)总是更优越。不幸的是,生物学和社会科学中的许多观察成果,不可能满足数学陈述所需要的条件,即坚定地忠诚于数学陈述规则 (imperative) 。
作出以下区分非常重要:一种是试图对一套丰富的证据作出数学陈述;另一种是一个数学模型,包含着各种发明出来解释某种旧有的现象或预测某种新现象的先验的辙念。开普勒(Kepler)的方程式是用来描述关于火星轨道的广泛的观察成果的。相反,弦理论家的各种方程式包含在未曾观察到的十维空间(tendimensions)中振动的能量包(packets of energy)的观念。如果某类现象既符合证据,又不需要设立太多违背已知事实的假设,以其内在本质而不是通过各种结果或后果来界定它的各种概念,这时,关于此类现象的数学模型更富有成效。比如,在牛顿描述一个下落的苹果的方程式中,时间和距离的物理概念有固定的定义,该定义独立于该落体的结局,也独立于其他从同一株树上落下的苹果所需要的距离和时间。
这些要求看起来可能平淡无奇,但不幸的是在进化生物学(evolutionary biology)和经济学这两个依赖形式模型的领域中,许多数学模型未能达到它们的要求。比如,一些进化论的模型假定可以繁殖无穷大的种群,在某种动物的基因(称为“异位显性”epistasis)中不存在彼此交互式的影响,这两种假定都违背已知的事实。假设为某种动物的最佳行为策略,制定一个进化论的模型,它包含以下五个概念:为了“一种资源”(食物或栖息地niche) 与某个竞争者竞争的“战斗成本”,把它与“逃跑”相比较,该资源的“价值”以及为该动物的“内含适应性”(inclusivefitness)制定的每个行为策略的种种含义。这任何一个概念都是从其功能上而不是从内在本质上来界定的。
一个观察两只鹰从远方接近同一个被掠食目标的生物学家,在两只鹰相遇前,不可能计算出与它们作出战斗或逃离的决策相关的战斗或退却的适应成本(cost to fitness),或每只鹰的适应性的变化。此外,如果该资源是一个用于构筑巢穴而不是用于获取食物的栖息地,那么该方程式中价值、成本和适应性的大小会发生变化。然而,令人惊讶的是,进化论生物学家在其各种抽象的模型中忽视了这些细节,未能详细说明所得到的或所失去的是不是食物,是不是接近交配对象的机会,是不是一个栖息处——这些都使各个方程式变得不明确,使人怀疑它们的普适性。
类似的问题也使人们怀疑许多经济学家的模型的价值。虽然我将在第四章详细考虑这个问题,但在这里举一个例子有助于理解。在温暖的6月的第一天,经过一个寒冷的春天后,几百万工人将需要作出选择:休假一天或尽自己的义务向某个雇主表示尊敬。在这种情况下,经济学家依赖于“优选权”(preference)的概念。这些工人们必须在两种不同的效用间作出选择,而这两种效用只有在每个工人完成所选择的事情后才能衡量。经济学家首先需要找出这一天去上班和不去上班的工人的比例,然后根据这一事实为这种情况发明一个数学模型。
这种局限性使人想起20世纪行为主义者所受到的挫折,他们也是依赖于“报酬”(reward)的概念,但没有一种内在定义使他们提前知道哪些现象拥有这种特殊的性质。心理学家必须等待并看到动物奋力获得的剌激物或处境(situations)是什么,然后根据这一事实称这些剌激物或处境为报酬。
请思考一下公认的一张关于经济学家的模型的漫画是怎样的。在对一个1000 人进行持续一年时间的实验的例子中,研究者可以测量每一个人反对或迎合其妻子、雇主或好朋友要求的场合的比例。设想证据表明,一般那些更经常地反对并较少满足其妻子要求的男人的平均数,更多地满足其雇主的要求但不向朋友表现出偏爱之意的人的平均数。草拟出一个总的模型,说明满足需要的效用超过了反对的成本,或说明反对的效用相当于他们选择这种应付三个情况的比例的平均数,都将是错误的。更准确地讲,优先选择一个而放弃另一个策略,是随着特定社会背景的不同而变化的。在经济学和生物学的模型中,没有给特殊性( specificity) 留下一个适当的位置。
许多经济学家忽视那些看上去并不正规的却具有解释力的模型,而是偏爱结构上以数学方式作出的解释,因为他们认为“经济学不能由它的主题而是由它的思维方式来界定”。诺贝尔经济学奖获得者罗伯特·卢卡斯(Robert Lutas)在这个问题上是一个更教条化的人。他说道:“经济理论就是数学分析。其他一切都只是些想象和漫谈。”
同样重要的是,生物学家和经济学家的模型假定加减乘除的算术规则,是以测量其各种概念的数字为基础的符合逻辑的运算规则。然而,可以质疑这一假定。物理的概念“质量”(mass)达到了数学标准,使得科学家能把两个不同物体的质量(比如说一段圆木和一块石头)相加而达到某个新的数值。这些标准包括比例尺的假定(即10公斤的质量等于5公斤的质量的两倍,200公斤的质量是100 公斤的质量的两倍)。然而,较不明确的是经济学家的概念“效用”(utility)是否满足这些要求。经济学家用武断的数量尺度来测量某种效用,就好像该效用具有质量的性质。比如,他们暗中把某位父亲所期望的为了周末和假期购买一辆新车的效用,与他们认为该父亲有意让女儿把这辆车用于上下班的效用加在一起。因为上述效用因心理上的差异而不同,所以这两种数值的总和与每一种效用的数值是不是成常比,这是不明显的,关于质量的问题也是这样。该父亲认为他的女儿每星期将有5 天时间使用这辆车,减少了他预期的在每周的周末使用它的效用,这是可能的。经济学家和进化论生物学家的形式模型中,没有一个概念具有物理学家的质量这个概念所具有的那些数学性质。
语义形式与图式形式
人文学者和社会科学家在深思一个问题及提出某种解决方法时,主要依靠各种语义网络和图式的形式,而不是各种数学概念。对诸如理想、启蒙运动、社会、身份和冲突之类的概念网络,无法用数学探讨的方法来处理。语义和图式的网络具有怂恿学者们根据各种要素的类型来思考的优势;数学方程式引导研究者根据各个单独特征的持续功能来思考问题。大部分罕见的事件都属于不连续(discrete) 的类型,产生于几个同时发生的但低概率(low-probabilíty) 的条件的结合,正如“完美风暴”(perfect stonns) 的发生。然而,在某个解决过程的某个点上,来自三个群体的大部分成员很可能会激活某些可感知的事件的表征(representations),这些事件正是他们的方程式和语义概念试图加以描述的。甚至弦理论家,他们是依赖数学陈述的,也画出图像来说明他们对一根弦的理解。所有这三种精神形式都是有用的,其窍门在于,知道什么时候使用每一种形式并避免在某个不合适的时机使用错误的工具。
容忍模糊性
各种数学的、语义的和图式的表达,在它们所传达的知识的模糊性(ambiguity)方面各不相同。可以按照描述和结论的模糊性的表现,把各门知识学科(intellectual disciplines) 安排成一个连续统(continuum),数学和物理学为一端,社会科学在当中,人文学科在另一端。因为个人对模糊性的容忍度不一样,所以个人性格特征和文化很可能影响着人们对某个领域的学术生涯的选择。一些年轻人继承了一种生理特征,当他们对未来感到不确定时,就特别容易受到某种不舒服的紧张感的袭击;当他们拥有某种选择权时,使良好的行为与不好的行为之间存在模糊性。许多具有此类性格特征的成年人像年轻的孩子那样异乎寻常地腼腆腆。伯特兰·罗素就是一个经常做噩梦的腼腆的年轻人,他毕生都在为驱除哲学中的模糊性而努力。
www.psychspace.com心理学空间网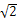 image004
image004 0
0
